Distance Tree solution(hard version)|codeforces round #769 (div 2)

                                          E2. Distance Tree (hard version)

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

This version of the problem differs from the previous one only in the constraint on n$n$.

A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The distance between two vertices is the minimum sum of weights on the path connecting them.

You are given a weighted tree with n$n$ vertices, each edge has a weight of 1$1$. Denote d(v)$d(v)$ as the distance between vertex 1$1$ and vertex v$v$.

Let f(x)$f(x)$ be the minimum possible value of max1≤v≤n d(v)$\underset{1\le v\le n}{max}d(v)$ if you can temporarily add an edge with weight x$x$ between any two vertices a$a$ and b$b$ (1≤a,b≤n)$(1\le a,b\le n)$. Note that after this operation, the graph is no longer a tree.

For each integer x$x$ from 1$1$ to n$n$, find f(x)$f(x)$.

Input

The first line contains a single integer t$t$ (1≤t≤104$1\le t\le {10}^4$) — the number of test cases.

The first line of each test case contains a single integer n$n$ (2≤n≤3⋅105$2\le n\le 3\cdot {10}^5$).

Each of the next n−1$n-1$ lines contains two integers u$u$ and v$v$ (1≤u,v≤n$1\le u,v\le n$) indicating that there is an edge between vertices u$u$ and v$v$. It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of n$n$ over all test cases doesn't exceed 3⋅105$3\cdot {10}^5$.

Output

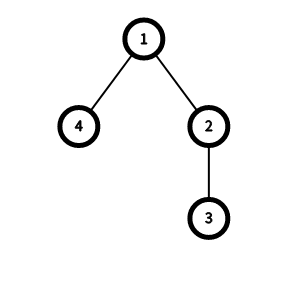
For each test case, print n$n$ integers in a single line, x$x$-th of which is equal to f(x)$f(x)$ for all x$x$ from 1$1$ to n$n$.

Note

In the first testcase:

• For x=1$x=1$, we can an edge between vertices 1$1$ and 3$3$, then d(1)=0$d(1)=0$ and d(2)=d(3)=d(4)=1$d(2)=d(3)=d(4)=1$, so f(1)=1$f(1)=1$.
• For x≥2$x\ge 2$, no matter which edge we add, d(1)=0$d(1)=0$, d(2)=d(4)=1$d(2)=d(4)=1$ and d(3)=2$d(3)=2$, so f(x)=2$f(x)=2$.

Solution link below:

if 1st link is not work then click on another link

solution link 1

https://afly.pro/X6gV2u4

Solution link 2

https://shrinke.me/0joa

Solution link 3

https://afly.pro/4dPM5oi